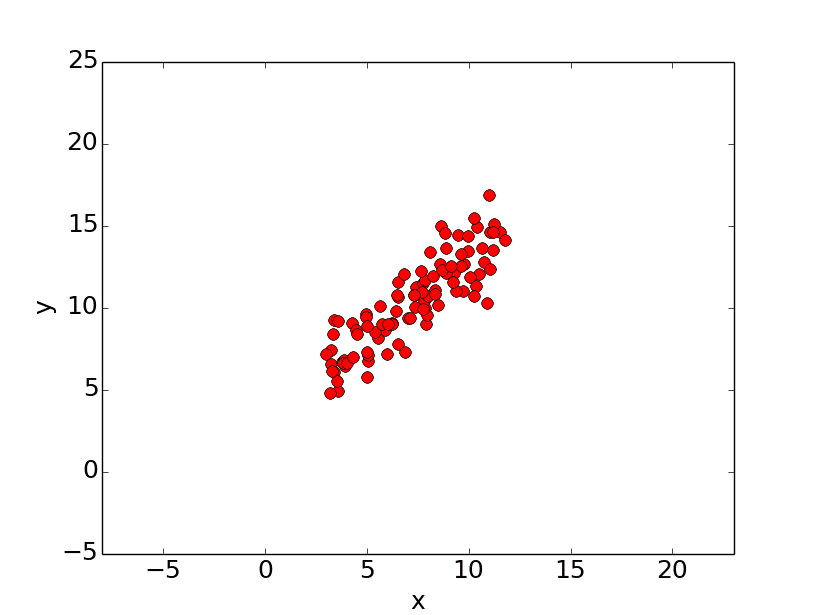
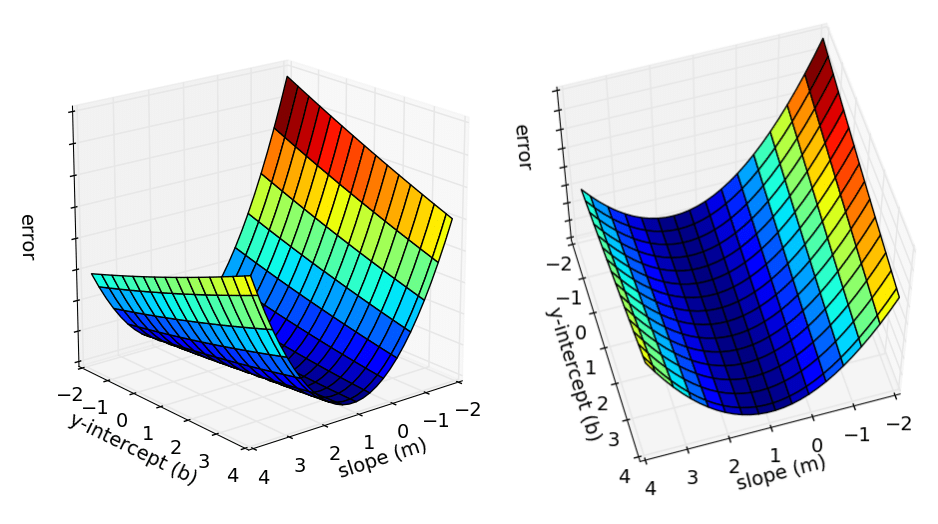
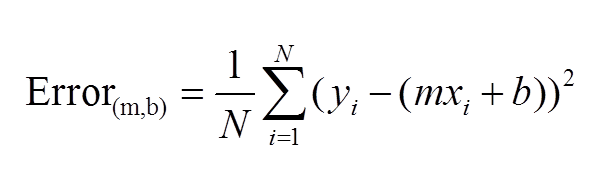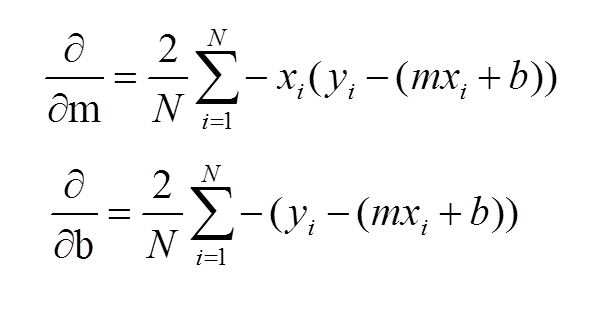Kezunlin's Blog

Live and Learn

0%

linear Regression with gradient descent

Posted on Edited on In

Tutorial

  • 目标
    给定N组二位坐标点对(x1,x2),…,(xn,yn)，拟合直线y = mx + b，找到最佳的m和b，使得总的误差最小。

  • 数据展示
    points

  • 误差公式
    errors

  • 可视化误差
    误差error是m和b的函数
    visual errors of m and b

  • 偏导数计算公式
    partial derivatives

  • 学习过程
    learning

  • 误差曲线
    errors curve

  • 动画演示
    演示链接

Gradient Descent

随机梯度示例

横轴X代表参数，纵轴Y代表误差。
gradient descent should force us to move in the direction of the minimum
hilly landscape

沿着曲线斜率slope移动

The best guess the algorithm can do is to move in the direction that of the slope, also called the gradient of the function.
move in the slope

单变量(single variable)

  • derivative:　导数是一个极限，准确值。
    derivative of single variable

  • estimated gradient: 梯度是一个估计值，和采样距离dx有关。
    estimated gradient

  • how to update parameter
    Once we have found our estimated derivative, we need to move in its opposite direction to climb down the function. This means that we have to update our parameter p like this:
    update parameter
    The constant L is often referred as learning rate, and it dictates how fast we move against the gradient.
    找到梯度之后，沿着梯度的相反方向移动。

多变量(multiple variable)

  • partial derivatives: 多变量偏导数
    partial derivatives
    partial derivatives
    partial derivatives

  • estimated gradient: 梯度和采样距离dx,dy,dz有关。
    estimated gradient
    estimated gradient
    estimated gradient

  • gradient vector: 梯度向量
    gradient vector

Code Example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
import numpy as np

# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (m * x + b)) ** 2
    return totalError / float(len(points))

def update_mini_batch(b, m, mini_batch, learningRate):
    #一次epoch梯度迭代，该函数需要调用epoches次
    #每一次计算m,b的梯度，每一次学习都需要所有的N个样本数据参与运算。一个epoch内，只能学习１次。
    #后续可以采用mini-batch思路，每一次学习只需要m个样本数据参与运算。一个epoch内，可以学习n/m次。
    N = float(len(points))
    b_gradient,m_gradient = compute_cost_gradient_of_all(mini_batch,b,m)
    new_b = b - (learningRate/N) * b_gradient
    new_m = m - (learningRate/N) * m_gradient
    return [new_b, new_m]

def compute_cost_gradient_of_all(points,b,m):
    #计算N个样本的总梯度
    b_gradient = 0
    m_gradient = 0
    for i in range(0, len(points)):
        delta_b,delta_m = compute_cost_gradient_of_one(points[i],b,m)
        b_gradient += delta_b
        m_gradient += delta_m
    return [b_gradient,m_gradient]

def compute_cost_gradient_of_one(point,b,m):
    #计算一个样本的梯度
    x = point[0]
    y = point[1]
    b_gradient =  -2 *     (y - ((m * x) + b))
    m_gradient =  -2 * x * (y - ((m * x) + b))
    return [b_gradient,m_gradient]

def gradient_descent_runner(points, starting_b, starting_m, learning_rate, epoches):
    b = starting_b
    m = starting_m
    for i in range(epoches):
        #每一次学习都需要所有的N个样本数据参与运算。一个epoch内，只能学习１次。
        #此时,mini_batch包含了所有N个样本。
        b, m = update_mini_batch(b, m, array(points), learning_rate)
        #print "{0} iterations b = {1}, m = {2}, error = {3}".format(i, b, m, compute_error_for_line_given_points(b, m, points))
    return [b, m]

def gradient_descent_runner_with_mini_batch(points, starting_b, starting_m, learning_rate, epoches,mini_batch_size):
    b = starting_b
    m = starting_m
    n = len(points)
    num_batches = n/mini_batch_size
    for i in range(epoches):
        #采用mini-batch思路，每一次学习只需要m个样本数据参与运算。一个epoch内，可以学习n/m次。

        # shuffle data and get N/mini_batch_size mini batches
        np.random.shuffle(points)

        # iterate over all mini batches to learn (updating m and b)
        # now in a epoch,we can learn N/mini times instead of just once.
        for k in xrange(0,num_batches):
            mini_batch = points[k*mini_batch_size : (k+1)*mini_batch_size]
            b, m = update_mini_batch(b, m, mini_batch, learning_rate)
        #print "{0} iterations b = {1}, m = {2}, error = {3}".format(i, b, m, compute_error_for_line_given_points(b, m, points))
    return [b, m]

def run():
    points = genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0 # initial y-intercept guess
    initial_m = 0 # initial slope guess
    epoches = 1000
    print "Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points))
    print "Running..."
    [b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, epoches)
    print "After {0} iterations b = {1}, m = {2}, error = {3}".format(epoches, b, m, compute_error_for_line_given_points(b, m, points))

def run2():
    points = genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0 # initial y-intercept guess
    initial_m = 0 # initial slope guess
    epoches = 1000
    mini_batch_size = 10 # mini batch size
    print "Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points))
    print "Running..."
    [b, m] = gradient_descent_runner_with_mini_batch(points, initial_b, initial_m, learning_rate, epoches,mini_batch_size)
    print "After {0} iterations b = {1}, m = {2}, error = {3}".format(epoches, b, m, compute_error_for_line_given_points(b, m, points))

if __name__ == '__main__':
    run()
    #run2()
Starting gradient descent at b = 0, m = 0, error = 5565.10783448
Running...
After 1000 iterations b = 0.0889365199374, m = 1.47774408519, error = 112.614810116

Reference

History

  • 20180806: created.