Tutorial
目标
给定N组二位坐标点对(x1,x2),…,(xn,yn),拟合直线y = mx + b,找到最佳的m和b,使得总的误差最小。数据展示
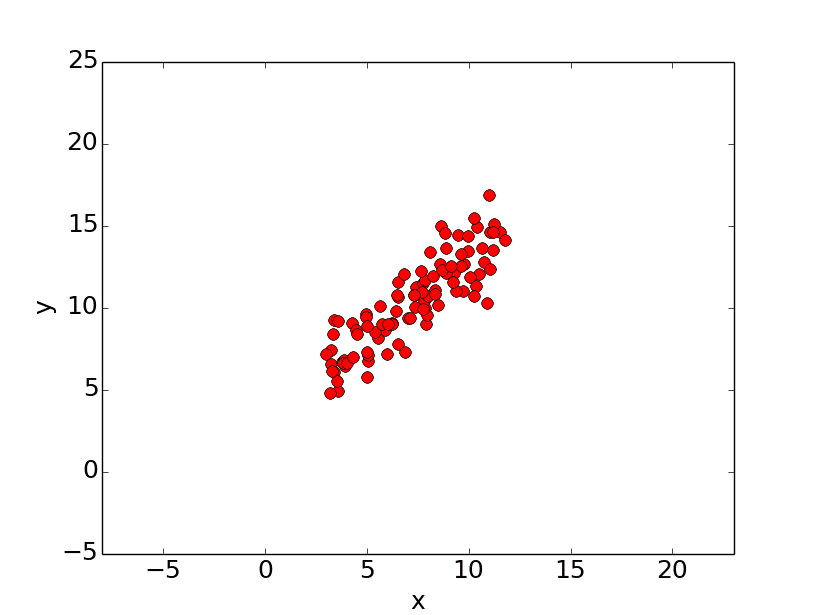
误差公式
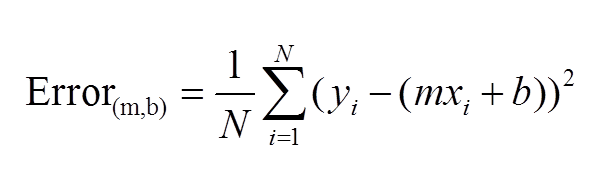
可视化误差
误差error是m和b的函数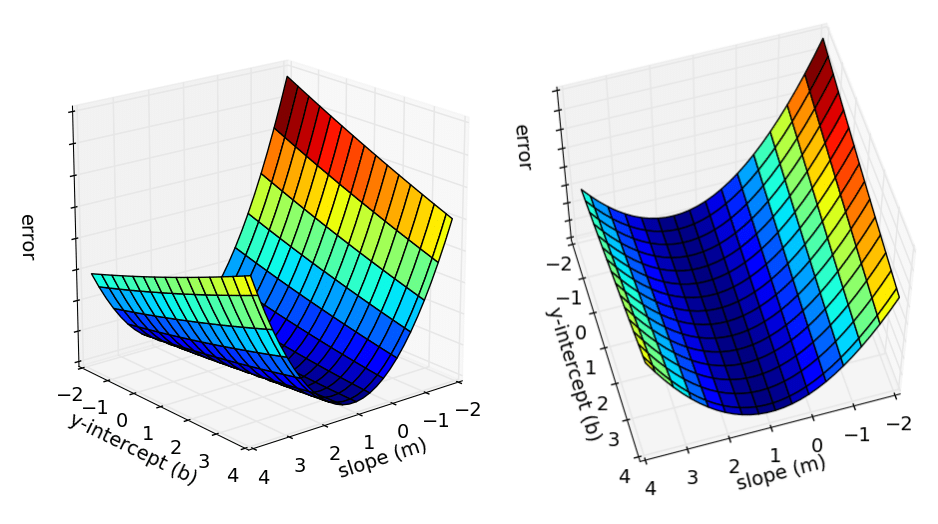
偏导数计算公式
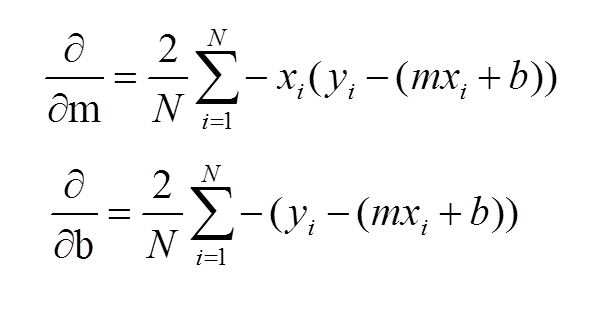
学习过程

误差曲线
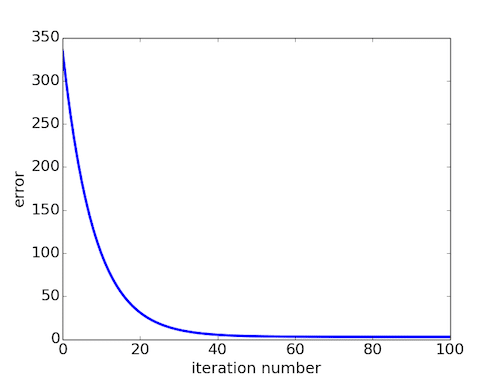
动画演示
演示链接
Gradient Descent
随机梯度示例
横轴X代表参数,纵轴Y代表误差。
gradient descent should force us to move in the direction of the minimum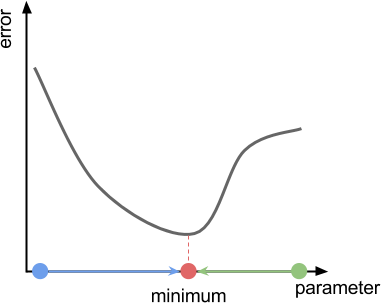
沿着曲线斜率slope移动
The best guess the algorithm can do is to move in the direction that of the slope, also called the gradient of the function.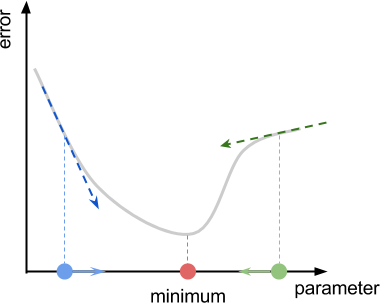
单变量(single variable)
derivative: 导数是一个极限,准确值。
estimated gradient: 梯度是一个估计值,和采样距离dx有关。
how to update parameter
Once we have found our estimated derivative, we need to move in its opposite direction to climb down the function. This means that we have to update our parameter p like this:
The constant L is often referred as learning rate, and it dictates how fast we move against the gradient.
找到梯度之后,沿着梯度的相反方向移动。
多变量(multiple variable)
partial derivatives: 多变量偏导数
estimated gradient: 梯度和采样距离dx,dy,dz有关。
gradient vector: 梯度向量
Code Example
#!/usr/bin/python
# -*- coding: utf-8 -*-
from numpy import *
import numpy as np
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (m * x + b)) ** 2
return totalError / float(len(points))
def update_mini_batch(b, m, mini_batch, learningRate):
#一次epoch梯度迭代,该函数需要调用epoches次
#每一次计算m,b的梯度,每一次学习都需要所有的N个样本数据参与运算。一个epoch内,只能学习1次。
#后续可以采用mini-batch思路,每一次学习只需要m个样本数据参与运算。一个epoch内,可以学习n/m次。
N = float(len(points))
b_gradient,m_gradient = compute_cost_gradient_of_all(mini_batch,b,m)
new_b = b - (learningRate/N) * b_gradient
new_m = m - (learningRate/N) * m_gradient
return [new_b, new_m]
def compute_cost_gradient_of_all(points,b,m):
#计算N个样本的总梯度
b_gradient = 0
m_gradient = 0
for i in range(0, len(points)):
delta_b,delta_m = compute_cost_gradient_of_one(points[i],b,m)
b_gradient += delta_b
m_gradient += delta_m
return [b_gradient,m_gradient]
def compute_cost_gradient_of_one(point,b,m):
#计算一个样本的梯度
x = point[0]
y = point[1]
b_gradient = -2 * (y - ((m * x) + b))
m_gradient = -2 * x * (y - ((m * x) + b))
return [b_gradient,m_gradient]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, epoches):
b = starting_b
m = starting_m
for i in range(epoches):
#每一次学习都需要所有的N个样本数据参与运算。一个epoch内,只能学习1次。
#此时,mini_batch包含了所有N个样本。
b, m = update_mini_batch(b, m, array(points), learning_rate)
#print "{0} iterations b = {1}, m = {2}, error = {3}".format(i, b, m, compute_error_for_line_given_points(b, m, points))
return [b, m]
def gradient_descent_runner_with_mini_batch(points, starting_b, starting_m, learning_rate, epoches,mini_batch_size):
b = starting_b
m = starting_m
n = len(points)
num_batches = n/mini_batch_size
for i in range(epoches):
#采用mini-batch思路,每一次学习只需要m个样本数据参与运算。一个epoch内,可以学习n/m次。
# shuffle data and get N/mini_batch_size mini batches
np.random.shuffle(points)
# iterate over all mini batches to learn (updating m and b)
# now in a epoch,we can learn N/mini times instead of just once.
for k in xrange(0,num_batches):
mini_batch = points[k*mini_batch_size : (k+1)*mini_batch_size]
b, m = update_mini_batch(b, m, mini_batch, learning_rate)
#print "{0} iterations b = {1}, m = {2}, error = {3}".format(i, b, m, compute_error_for_line_given_points(b, m, points))
return [b, m]
def run():
points = genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
epoches = 1000
print "Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points))
print "Running..."
[b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, epoches)
print "After {0} iterations b = {1}, m = {2}, error = {3}".format(epoches, b, m, compute_error_for_line_given_points(b, m, points))
def run2():
points = genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
epoches = 1000
mini_batch_size = 10 # mini batch size
print "Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points))
print "Running..."
[b, m] = gradient_descent_runner_with_mini_batch(points, initial_b, initial_m, learning_rate, epoches,mini_batch_size)
print "After {0} iterations b = {1}, m = {2}, error = {3}".format(epoches, b, m, compute_error_for_line_given_points(b, m, points))
if __name__ == '__main__':
run()
#run2()
Starting gradient descent at b = 0, m = 0, error = 5565.10783448
Running...
After 1000 iterations b = 0.0889365199374, m = 1.47774408519, error = 112.614810116
Reference
History
- 20180806: created.



